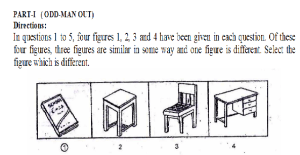
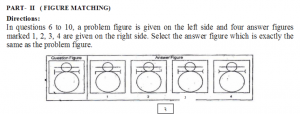
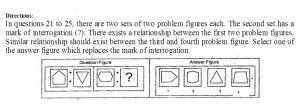
JNVST Model Paper 2024 Download with Navodaya Previous Paper 2024 Pdf JNVST Subject wise Syllabus 2024 for 5th to 6th Class Admission Test Details is Mental Ability Test, English Languages, Arithmetic Test etc, JNVST 5th to 11th Class Syllabus 2024 Details is English, Hindi, Maths, Science etc,
JNVST 5th, 6th, 9th, 11th Model Paper 2024

JNVST 2024 Practice Questions Sets and Solved Papers 2024, So Download Navodaya Vidyalaya Exam Prepare for Entrance Examination. Model Question Papers are Also Given Below Details is JNVST Class 5th, 6th Solved Papers JNVST Solved Papers Sets Class Vth to 11th, JNVST Practice Sets for Class 5th to IXth in Hindi,
JNVST Class 5th 6th 8th 9th 11th Practice Sets, JNVST Class 9th Solved Papers, JNVST Exam Practice Work Book Combo JNVST Exam Pattern 2024 Question pattern or Paper Style etc,